# 题目描述
给你一个 n x n 整数矩阵 grid ,请你返回 非零偏移下降路径 数字和的最小值。
非零偏移下降路径 定义为:从 grid 数组中的每一行选择一个数字,且按顺序选出来的数字中,相邻数字不在原数组的同一列。
提示:
n == grid.length == grid[i].length1 <= n <= 200-99 <= grid[i][j] <= 99
# 测试用例
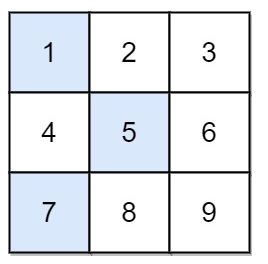
输入:
grid = [[1,2,3],[4,5,6],[7,8,9]]输出:13
解释: 所有非零偏移下降路径包括:
[1,5,9], [1,5,7], [1,6,7], [1,6,8],[2,4,8], [2,4,9], [2,6,7], [2,6,8],[3,4,8], [3,4,9], [3,5,7], [3,5,9]
下降路径中数字和最小的是[1,5,7] ,所以答案是 13 。
# 思路
动态规划
一行一行的遍历元素,看要还是不要得到的和最小
# 代码实现
/**
* @param {number[][]} grid
* @return {number}
*/
var minFallingPathSum = function (grid) {
// dp[i][j]表示从数组 grid 的前 i 行 并且 第 i 行选grid[i][j] 得到的最小值
const n = grid.length;
const dp = new Array(n)
.fill(0)
.map(() => new Array(n).fill(Number.MAX_SAFE_INTEGER));
for (let i = 0; i < n; i++) {
dp[0][i] = grid[0][i];
}
// i 是行
// j 是列
for (let i = 1; i < n; i++) {
for (let j = 0; j < n; j++) {
for (let k = 0; k < n; k++) {
if (j === k) {
continue;
}
// 不走 j == k 的情况
dp[i][j] = Math.min(dp[i][j], dp[i - 1][k] + grid[i][j]);
}
}
}
console.log("dp: ", dp);
console.log("dp[n - 1]: ", dp[n - 1]);
return Math.min(...dp[n - 1]);
};
var __readline = require("readline-sync");
__readline.setDefaultOptions({ prompt: "" });
var readline = __readline.prompt;
console.log("请输入二维数组grid的行数: ");
const row = readline();
console.log("请按行输入二维数组: ");
/*
请输入二维数组grid的行数:
3
请按行输入二维数组:
1,2,3
4,5,6
7,8,9
dp: [ [ 1, 2, 3 ], [ 6, 6, 7 ], [ 13, 14, 15 ] ]
dp[n - 1]: [ 13, 14, 15 ]
结果为: 13
*/
let grid = [];
for (let i = 0; i < row; i++) {
let arr = readline()
.split(",")
.map((item) => parseInt(item));
grid.push(arr);
}
const res = minFallingPathSum(grid);
console.log("结果为: ", res);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67