题目描述

叶值的最小代价生成树

给你一个正整数数组 arr，考虑所有满足以下条件的二叉树：

• 每个节点都有 0 个或是 2 个子节点。
• 数组 arr 中的值与树的中序遍历中每个叶节点的值一一对应。
• 每个非叶节点的值等于其左子树和右子树中叶节点的最大值的乘积。

在所有这样的二叉树中，返回每个非叶节点的值的最小可能总和。这个和的值是一个 32 位整数。

如果一个节点有 0 个子节点，那么该节点为叶节点。

提示:

• 2 <= arr.length <= 40
• 1 <= arr[i] <= 15
• 答案保证是一个 32 位带符号整数，即小于 231

测试用例

用例1：

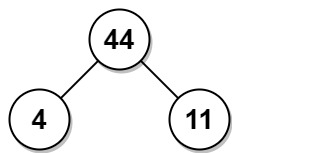
• 输入：arr = [6,2,4]
• 输出：32
• 解释：有两种可能的树，第一种的非叶节点的总和为 36 ，第二种非叶节点的总和为 32 。

用例2：

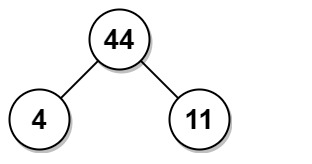
• 输入：arr = [4,11]
• 输出：44

思路

因为每个节点都有0个或2个子节点，同时是中序遍历，所以可以把arr分割成两部分，一部分是左子树，一部分是右子树

区间动态规划

• dp[i][j]表示arr[i...j]合并后的最小乘积之和
• dp[0][len]就是arr的最小代价

dp[i][j] = 左子树非叶节点最小(dp[i][k]) + 右子树非叶节点最小(dp[k + 1][j]) + 根节点（左边和右边的最大值的乘积，）

代码实现

/**
 * @param {number[]} arr
 * @return {number}
 */
var mctFromLeafValues = function(arr) {
    // 因为每个节点都有0个或2个子节点，同时是中序遍历
    // 所以可以把arr分割成两部分
    // 一部分是左子树，一部分是右子树

    // 动态规划
    // dp[i][j]表示arr[i...j]合并后的最小乘积之和
    // dp[0][len]就是arr的最小代价

    // [1, 2, 3, 4, 5, 6, 4, 3, 3, 2];

    // maxVal[i][j]怎么理解

    const n = arr.length;
    const dp = new Array(n).fill(0).map(() => new Array(n).fill(0));
    const maxVal = new Array(n).fill(0).map( () => new Array(n).fill(0) );

    // 求arr从i到j之间元素的最大值，i <= j
    // for(let i = 0; i < n; i ++){
    //     maxVal[i][i] = arr[i];
    //     for(let j = i + 1; j < n; j ++){
    //         // 从前往后遍历，得到i到j之间的arr最大值
    //         maxVal[i][j] = Math.max(maxVal[i][j - 1], arr[j]);
    //     }
    // }

    for(let i = 0; i < n; i ++){
        let max = arr[i];
        for(let j = i; j < n; j ++){
            max = Math.max(max, arr[j]);
            maxVal[i][j] = max;
        }
    }

    console.log("maxVal: ", maxVal);
    // for(let j = 0; j < n; j ++){
    //     for(let i = j; i >= 0; i --){
    //         // 枚举i到j之间的k，i <= k < j
    //         min = Number.MAX_SAFE_INTEGER;
    //         for(let k = i; k < j; k ++){
    //             // 枚举k，然后不断更新根结点值和左右子树值和的最小值
    //             // 注意这里的min，也是要实时更新的
    //             // 不能每次都跟Number.MAX_SAFE_INTEGER来比较
    //             min = Math.min(min, dp[i][k] + dp[k + 1][j] + (maxVal[i][k] * maxVal[k + 1][j]));
    //             dp[i][j] = min;
    //         }
    //     }
    // }

    // dp[0][0], dp[1][1]这些是没有意义的，因为这种情况是没有非叶节点
    for(let len = 1; len < n; len++) {
		for(let i = 0; i + len < n; i++) {
			dp[i][i + len] = Number.MAX_SAFE_INTEGER;
			for(let k = i; k < i + len; k++) {
				dp[i][i+len] = Math.min(dp[i][i + len], dp[i][k] + dp[k+1][i+len] + maxVal[i][k] * maxVal[k+1][i+len]);
			}
		}
	}
    console.log("dp: ", dp);
    return dp[0][n - 1];
};